1.选择单位，简化数字计算

例1.将“220V 60W”灯泡接到220V的电路中，通电5小时，电流所做的功是多少度？

解析：1度＝1千瓦时，题中时间单位采用“小时”，所以相应采用“千瓦”作为功率单位，计算起来就简单得多。即P＝60W＝0.06kW，t＝5h，所以

度

2.选择公式，简化单位换算

例2.的物体浸没在水中，受到的浮力是多少？

解析：根据阿基米德原理，物理受到浮力等于它排开的水受的重力，而重力与质量有关，所以可先计算出排开水的质量，水的密度可用带入，便可避免体积单位换算和指数运算。即：，则。

3.等效法

例3.如图所示，将质量为的铜块放置于漂浮在水面上的木块上，恰能使木块全部浸入水中，而铜块仍留在空气中，如果把质量为的铜块挂在木块下面，也恰能使木块全部浸入水中，求与的质量比。（）

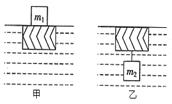
解析：等效法可以摒弃许多推导过程，道理简单易懂，用来解决“复合体”问题，不失为一条捷径。

图中铜块放在木块的上面和铜块挂在木块的下面，都使木块恰能全部浸入水中，其效果完全相同。则对木块的压力等于对木块的拉力，即。

所以，即

由和的值即可得出结论：。

4.假设法

例4.甲灯标有6V，乙灯标有2W，甲、乙两灯电阻分别为和，且，将两灯以某种方式连在电压为的电源上，两灯均正常发光，以另一种方式连在电压为的电源上，乙灯正常发光，甲灯功率只有其额定功率的，请问甲灯和以乙灯两次分别是怎样连接的？

解析：解答本题的关键是准确判断甲乙两灯先后连接的方式，很多同学对此一筹莫展，其实若用假设法，问题可迎刃而解。

假设：第一种连接方式为甲乙两灯并联，由两灯均正常发光，可推出：；

由第二种连接方式甲乙两灯串联，乙灯正常发光，，可推出：

进而推出：

这与题设矛盾，故这样假设是错误的，所以两灯一定是先串联后并联。

5.等量代换法

例5.如图2的电路中，已知，电压表的示数分别为60V、24V，求：。

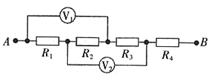
解析：四个电阻串联，电流相等，由的阻值相等，知其两端的电压必相等，即有。电压表测的是两端的电压和，测的是两端的电压和，作等量代换，则两端的电压和等于的示数，故等于两电压表示数之和，。

6.比例法

例6.甲、乙两块用同种物质制成的质量相等的金属块，加热到温度为℃后分别投入水和油中，能使质量为、温度为℃的水温度升高到℃，使质量为、温度为℃的油温度升高到℃，求这种油的比热容。

解析：此题有两个物理过程，即金属块与水相混合、金属块与油相混合。

设金属块的比热容为，质量为，油的比热容为。根据，可得下列两方程：

若根据<1>式列出的代数式，再代入<2>式计算，这样的计算会比较复杂。若采用比例的形式的约掉，则可省去复杂的数学计算。最后求得这种油的比热容约为。

此种方法多适合于题设中告诉两种物理过程的计算题。如热学中两次升温降温，电学中断开、闭合开关等。解答此类计算题的常见方法是，先分别根据两种物理过程列出相应的等量关系，然后采用两式的比求解。

7.方程组法

例7.在测定液体密度时，有一同学测出了液体的体积，容器和液体的总质量，实验做了两次记录如表：

液体的体积（）

5.8

7.9

容器和液体的总质量（g）

10.7

12.8

试求：（1）液体的密度；（2）容器的质量。

解析：要测液体的密度，常规做法是用天平测出液体的质量，用量筒（或量杯）量出液体体积，然后用求出。但这里由于两次测量都没有测出容器的质量，而无法求出液体的质量。

可设液体密度为，容器质量为m，根据和题设中条件可得方程组

解方程组得：

除此之外的解题方法还有理想模型法、隔离法、极值法、过程法、守恒法、图象法、讨论法等等，在解答计算题的过程中，如果能灵活运用合适的方法，就能避开繁琐的求解过程，迅速、准确地得到答案。